UNIVERSITÀ DEGLI STUDI ROMA TRE
FACOLTÀ DI SCIENZE M.F.N.
Tra "suono" e "rumore", per uno studio dinamico delle vocali
parlate e cantate
Sintesi della tesi di Laurea in Matematica
Di Stefania De Nittis
Relatore: Prof.ssa Laura Tedeschini Lalli
Oggetto della ricerca
L’oggetto di ricerca della tesi sperimentale è costituito dalla descrizione del segnale vocale con strumenti matematici differenti dagli usuali; ovvero tramite le tecniche di elaborazione del segnale proprie della teoria dei Sistemi Dinamici , in particolare la tecnica di Embedding.
La Tesi
Nel Cap.1 viene data una panoramica sui concetti fondamentali dei Sistemi dinamici trattati nella tesi e sul trattamento scientifico della voce; il Cap.2 analizza la "voce" dall’anatomia dell’apparato vocale alle teorie e tecniche di produzione del segnale vocale; il Cap. 3 illustra il Caos come alternativa al "rumore"; il Cap. 4 espone la tecnica di acquisizione dei dati sperimentali e ne accenna le tecniche di elaborazione classica; il Cap. 5 espone in dettaglio la metodologia utilizzata nella ricerca: l’Embedding; il Cap. 6 descrive gli esponenti di Lyapunov; il Cap. 7 mostra la ricerca sperimentale con metodi, analisi, elaborazione di dati e risultati. Le caratteristiche tecniche degli strumenti utilizzati sono fornite nel capitolo Schede Tecniche, i termini di maggior interesse sono in un breve Glossario, ed infine, i listati dei programmi da me elaborati ed utilizzati, sono raccolti nell’Appendice.
Presupposti, ipotesi e scopo della ricerca
Nel lavoro di ricerca si analizza il segnale vocale studiandone alcune componenti "elementari", in particolare alcune vocali: a, é, i ,ò, u.
L’emissione è eseguita dallo stesso soggetto che è in grado di governare, tramite la tecnica vocale, il sistema di filtraggio applicato al segnale successivamente al passaggio nella glottide. I dati sono campionati in serie temporali, le quali vengono immerse in uno spazio delle fasi a coordinate delays.
L’analisi del segnale vocale, effettuata fino ad oggi, si è basata prevalentemente su tecniche di elaborazione del segnale, illustrate nel Cap. 4, che partono dal presupposto che il segnale vocale sia armonico e lineare, cioè ben approssimabile con una serie finita di funzioni armoniche e tale che possa essere descritto da equazioni differenziali lineari.
Presupporre che le equazioni che descrivono il segnale siano lineari equivale ad affermare che il segnale non varia nel tempo. Ciò, è "abbastanza" vero per strumenti musicali prodotti dall’uomo, ma è decisamente falso per la voce umana, la cui intonazione non è fissa nel tempo. L’apparato produttore della voce, oltre ad essere molto complesso e ancora non del tutto capito, è difficilmente "gestibile" con precisione e soggetto a continue e molteplici variazioni determinate, come sottolineato nel Cap. 2, da più fattori, primo fra tutti quello emozionale, che lo rendono poco controllabile.
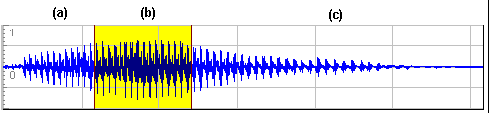
Inoltre le vocali sono state sempre trattate come periodiche, quando in realtà sono segnali non completamente periodici ed inoltre contaminati dal rumore; un segnale sonoro considerato "elementare", come per esempio una vocale, non solo non è periodico, ma possiede una parte relativa all’attacco (transitorio di attacco), una dove assume un andamento quasi periodico (quasi-stazionarietà) e un’altra di decadimento (transitorio di decadimento), come illustrato più dettagliatamente nel Cap. 2 e visualizzato nella fig.1
Attualmente la descrizione delle peculiarità del suono è fornita sia in termini di aspetti legati alla sua percezione uditiva, sia in termini di osservazioni nei domini del tempo e della frequenza; quindi usando come strumento di valutazione ed analisi o quello fisiologico, comunemente detto "orecchio", coadiuvato dalle capacità empiriche di esperti del settore ( cantanti, insegnanti di canto, linguisti, ecc.), o quello prettamente tecnico che utilizza strumenti forniti dalla matematica, fisica, ingegneria. Purtroppo, però, non esiste al momento la possibilità di collegare direttamente le sensazioni uditive con precise osservazioni fisiche. Da quanto ci risulta, inoltre, la voce non è mai stata analizzata con i metodi dei Sistemi dinamici, i quali studiano il comportamento di fenomeni a "metà strada" tra sistemi lineari con orbite periodiche e rumore, dove riteniamo, proprio, di collocare il segnale vocale per le sue caratteristiche temporali oggettive; precisiamo d’altronde che, attualmente, si ignora ed è ancora oggetto di ricerca, il sistema dinamico che produce il segnale vocale.
Le ipotesi considerate più probabili sul meccanismo mediante il quale la laringe trasforma il flusso espiratorio, prodotto dal mantice polmonare e spinto e modulato dal diaframma, in suono, si raccolgono in quattro teorie accennate nel Cap.2.
Fig. 1 Grafico di una componente "elementare" del segnale vocale: la vocale A, sezionata approssimativamente nelle tre fasi: a) Transitorio di attacco; b) Quasi-stazionarietà; c) Transitorio di decadimento. (La suddivisione è approssimata).

Sottoliniamo, inoltre, che, spesso, ricerche sul suono di tipo scientifico sono compiute da studiosi qualificati o nelle sole discipline scientifico-tecnologiche o nel campo musicale e vocale.
Il presente lavoro nasce, quindi, dalla constatazione della carenza di ricerche di tipo sperimentale sulla voce come segnale vocale non totalmente armonico, non completamente periodico e non lineare, ed effettuate da persone sufficientemente competenti in entrambi i settori scientifico e musicale, con l’intento di ricavare informazioni ulteriori a quelle possibili tramite le tecniche tradizionali di elaborazione del segnale.
Impostando la voce in modo differente, varia il colore del suono, ma, fatta eccezione per dei casi limite, rimane invariata la riconoscibilità delle vocali. Da qui la ricerca di un modello matematico interpretativo che le descriva e che colleghi le sensazioni uditive con precise osservazioni fisiche, sfruttando, oltre agli strumenti matematici propri dei Sistemi dinamici, le mie conoscenze e la mia esperienza di cantante. Queste ultime sono state di estrema utilità nel produrre il segnale quasi totalmente privo di effetti rumorosi, nell’isolare la regione di variazione della pronuncia delle vocali e nell’individuazione dei risultati.
Il risultato della ricerca è l’esistenza di una relazione tra aperture diverse interne nel tratto vocale, effettuate per produrre vocali diverse, e spazio delle fasi relativo alle suddette vocali. Questo apre nuove possibilità al modellamento matematico del segnale, tenendo conto di diversi gradi di libertà.
L’alta sensibilità del microfono, utilizzato per registrare i dati, ha permesso di catturare sia una maggiore gamma di frequenze, quindi dei dati quanto più possibile vicini alla realtà, sia, purtroppo, il rumore esterno che li ha inevitabilmente contaminati. Per diminuire una delle cause del rumore, ho controllato l’emissione con la tecnica vocale, generando un suono scevro da soffio. Ho campionato ogni segnale a 32 KHz con dimensione di campionamento a 16 bits, rispettando la condizione del Teorema di Shannon
![]() (1)
(1)
(![]() = periodo di
campionamento;
= periodo di
campionamento; ![]() = frequenza più alta del
segnale), per non perdere dei dati significativi. La voce femminile arriva anche a
frequenze superiori a 15 Khz, ma le alte frequenze si ottengono con i suoni molto acuti (sopracuti),
che riguardano prettamente la voce cantata in tonalità liriche molto alte che non ho
considerato per la ricerca.
= frequenza più alta del
segnale), per non perdere dei dati significativi. La voce femminile arriva anche a
frequenze superiori a 15 Khz, ma le alte frequenze si ottengono con i suoni molto acuti (sopracuti),
che riguardano prettamente la voce cantata in tonalità liriche molto alte che non ho
considerato per la ricerca.
.
Per poter elaborare i dati ho dovuto costruire un programma che trasforma i file da wav a txt. La descrizione in dettaglio e le verifiche sono nel Cap. 7.
Partendo da dati monodimensionali, cioè relativi alla sola variabile ![]() , pressione dell’aria, ne ho effettuato
l’immersione, con la tecnica di Embedding, in uno spazio tridimensionale
(visualizzandone due dimensioni per volta), con un programma che legge i dati da file di
tipo wav e li memorizza in un vettore di interi
, pressione dell’aria, ne ho effettuato
l’immersione, con la tecnica di Embedding, in uno spazio tridimensionale
(visualizzandone due dimensioni per volta), con un programma che legge i dati da file di
tipo wav e li memorizza in un vettore di interi ![]() , dove
, dove ![]() ed
ed ![]() è il numero di campionature lette, poi trasferisce i valori in tre
vettori delays secondo il metodo dei delays, ovvero con uno sfasamento del tempo
delay
è il numero di campionature lette, poi trasferisce i valori in tre
vettori delays secondo il metodo dei delays, ovvero con uno sfasamento del tempo
delay ![]() con
con ![]() coefficiente di sfasamento scelto, a valore intero, cioè
coefficiente di sfasamento scelto, a valore intero, cioè
|
per ![]() .
.
Se effettuo, per maggiore comprensione, un cambiamento di variabile
ponendo ![]() , il punto del ritratto delle fasi
all’iterata
, il punto del ritratto delle fasi
all’iterata ![]() -ma,
-ma, ![]() , avrà coordinate
, avrà coordinate
![]() (3)
(3)
Considerando, inoltre, che ogni campionatura ![]() è rilevata a distanza di tempo
è rilevata a distanza di tempo ![]() da
da ![]() si ha che al tempo
si ha che al tempo ![]()
![]() (4)
(4)
che sono proprio le coordinate delays con tempo delays ![]() .
.
Fig 2 Porzione di segnale campionato relativo alle vocali, nella fase di quasi-stazionarietà

Fig 3 Ritratto delle fasi delle vocali A, E (chiusa), O (aperta);
nella fase di transitorio di attacco, con coefficiente di sfasamento ![]() = 4.
= 4.
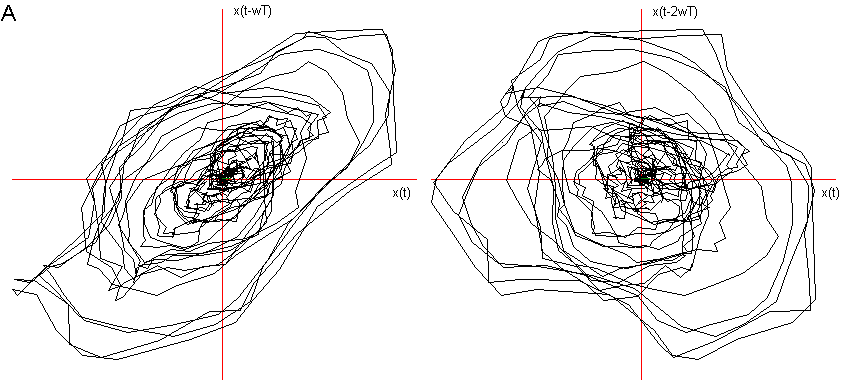
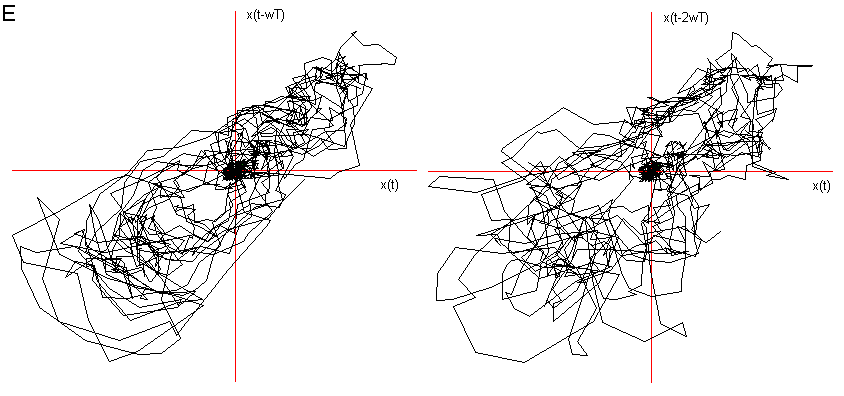
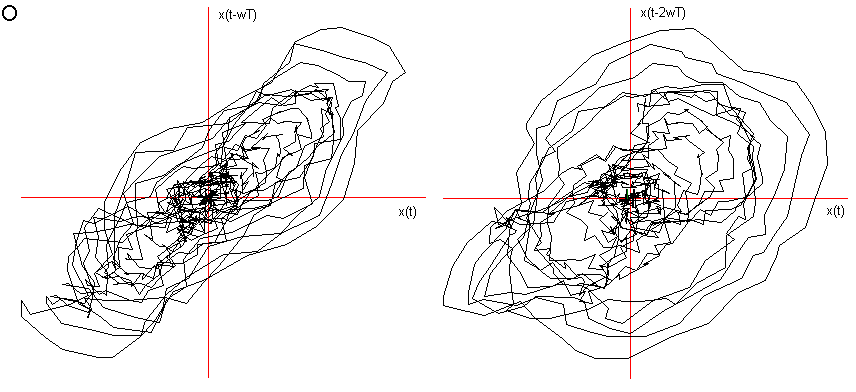
Ho considerato le prime due delle tre fasi caratteristiche descritte nel Cap 2 (Il segnale vocale) ed ho immerso in tre dimensioni 1000 campionamenti relativi al transitorio di attacco, leggendo i dati dalla prima campionatura, e 1000 alla fase di quasi-stazionarietà iniziando a leggere i dati dopo circa 3000 campionature. Nelle figg.3 e 4 sono visualizzati i risultati. Si vede chiaramente che il segnale nel transitorio di attacco tende verso una quasi-orbita descritta nella fase successiva di quasi-stazionarietà. La fase di quasi stazionarietà è tanto più vicina all’essere un attrattore, quanto più il segnale è prodotto con suono pulito, poco contaminato dal rumore e cantato, come si può constatare confrontando le figg. 4, 5 e 6.
Fig 4 Ritratto delle fasi delle vocali nella fase di quasi-stazionarietà,
effettuando l’embedding con coefficienti di sfasamento ![]() differenti per ogni vocale.
differenti per ogni vocale.
A dopo 3000 campionature e ![]() = 4.
= 4.

E dopo 3000 campionature e ![]() = 6.
= 6.
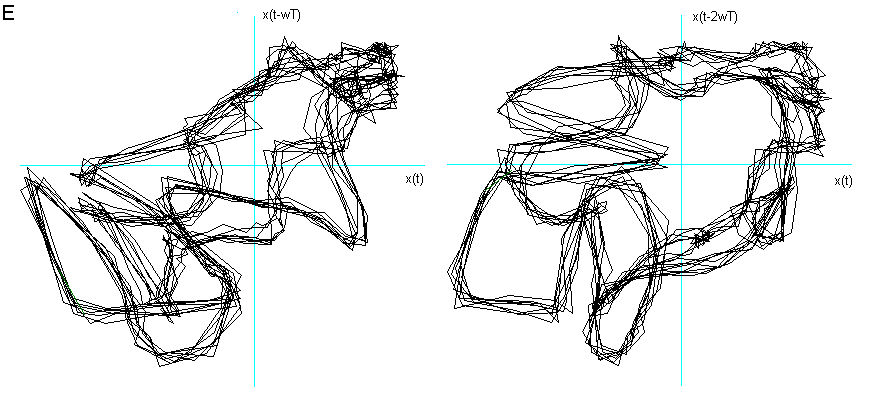
I dopo 3500 campionature e ![]() = 3.
= 3.
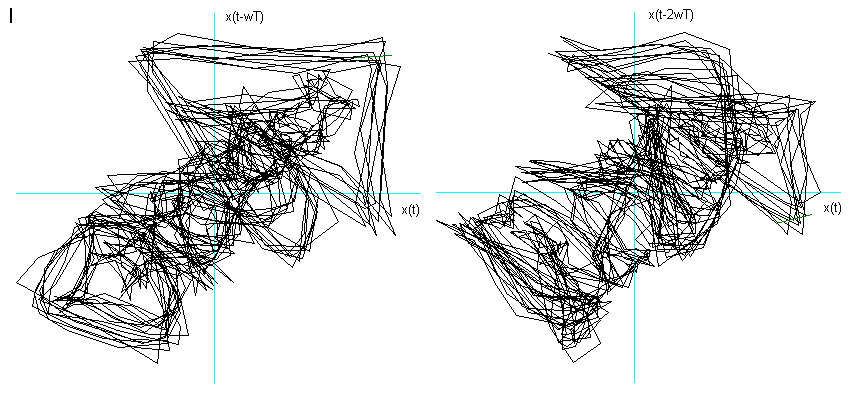
O dopo 3000 campionature e ![]() = 5.
= 5.
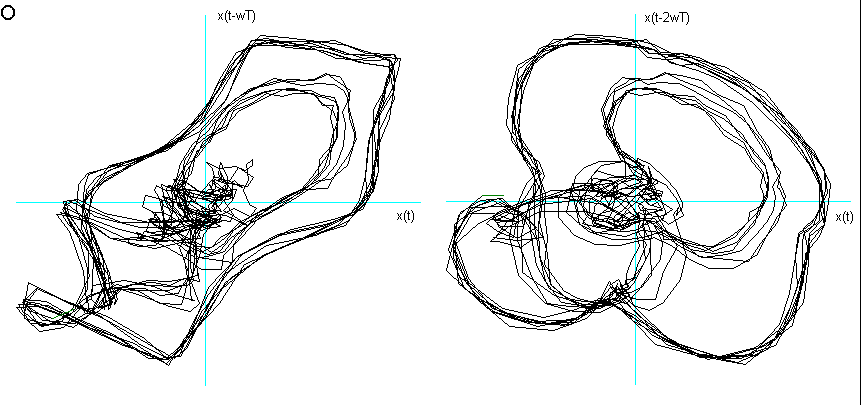
U dopo 3000 campionature e ![]() = 7.
= 7.
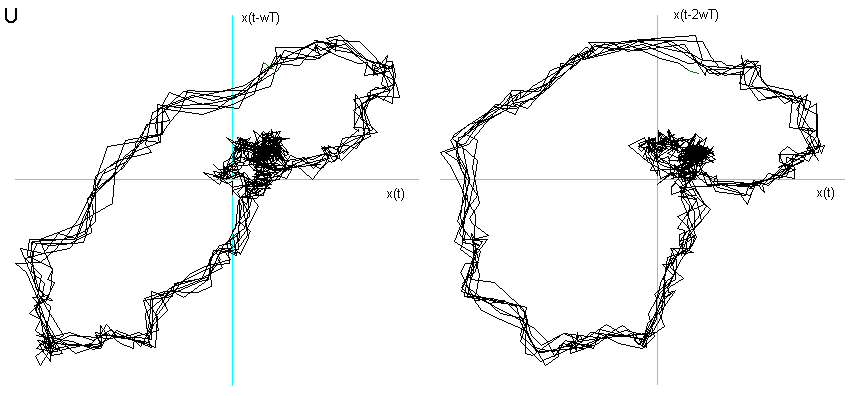
La scelta del coefficiente di sfasamento è stata compiuta dando a ![]() valori interi, da 1 in poi, fino ad ottenere
l’immagine meno distorta possibile: nel Cap. 5 viene discussa la relazione tra il periodo
di campionamento e la distorsione del ritratto delle fasi risultante. Il valore
ottimale di
valori interi, da 1 in poi, fino ad ottenere
l’immagine meno distorta possibile: nel Cap. 5 viene discussa la relazione tra il periodo
di campionamento e la distorsione del ritratto delle fasi risultante. Il valore
ottimale di ![]() risulta differente per ogni
vocale.
risulta differente per ogni
vocale.
Fig 5
La vocale A nella fase di quasi stazionarietà parlata e "sporca".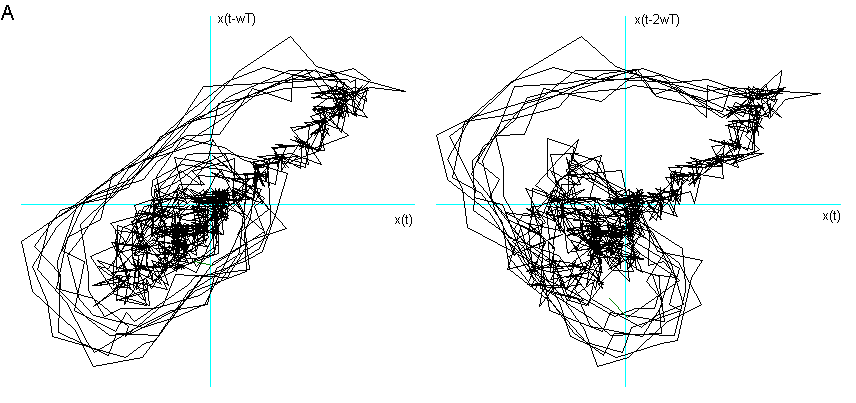
Per stabilire la dimensione di Embedding occorreva calcolare gli
esponenti di Lyapunov. L’alta contaminazione dei dati sperimentali e
l’insufficiente qualità degli strumenti meccanici ha dato risultati che necessitano
ulteriori approfondimenti con apparecchiature più sofisticate ed altri strumenti dei Sistemi
dinamici. Il procedimento successivo, è stato, quindi, quello suggerito nel cap. 5
cercando il minimo valore di ![]() per cui non si
verificano autointersezioni delle orbite descritte dal segnale discretizzato
per cui non si
verificano autointersezioni delle orbite descritte dal segnale discretizzato ![]() . Tale valore minimo è il valore della
dimensione di Embedding.
. Tale valore minimo è il valore della
dimensione di Embedding.
Per le vocali si è trovato![]() , per la U, in un caso particolare, è stato sufficiente
, per la U, in un caso particolare, è stato sufficiente ![]() , per alcune consonanti
, per alcune consonanti ![]() .
.
Analisi dei dati elaborati
Per analizzare ed estrapolare dei risultati significativi mi sono concentrata sulle sole vocali e nella fase di di quasi-stazionarietà del segnale. Questo poiché alcune consonanti avrebbero richiesto una dimensione di Embedding superiore ed avrebbero avuto una componente più alta di contaminazione dal rumore. A tal proposito fornisco un esempio di due consonanti: la M e la S, mostrandone il ritratto delle fasi nella fig. 6. La prima è semivocalica e risuona nelle fosse nasali, quindi contiene un’alta percentuale di suono "vocalico" se eseguita con una tecnica sufficientemente corretta, la seconda è spirante e contiene un’alta percentuale di soffio che determina un segnale molto "rumoroso".
La scelta dello studio della vocale nella fase di quasi-stazionarietà, piuttosto che nella sua "globalità", è invece dettata dall’intento di estrarre risultati sulle caratteristiche peculiari di ciascuna vocale, che si presuppone "quasi stabile" proprio in tale fase, e possibilmente in modo "visibilmente" chiaro.
Ad una prima osservazione appare evidente come ciascuna vocale sia caratterizzata da una sua particolare forma nello spazio delle fasi.
Fig. 6
Ritratto delle fasi della consonante semivocalica nasale M e spirante S.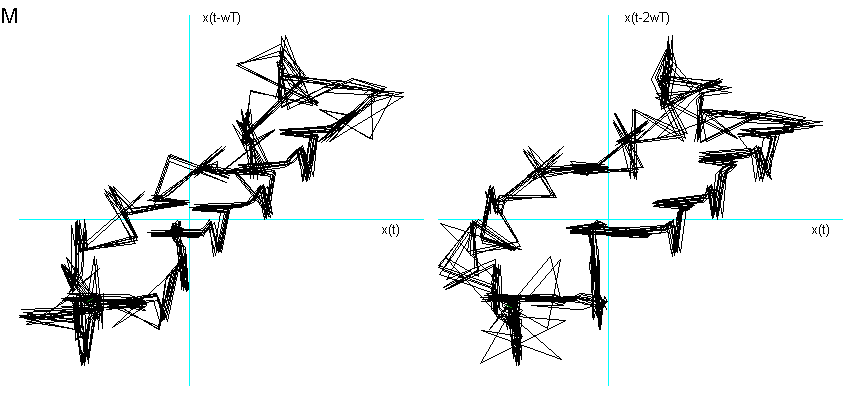

Esaminando la vocale A (fig. 7), prodotta in due tonalità differenti, nella fase di quasi stazionarietà, ed effettuando l’Embedding con lo stesso tempo delay, il suo ritratto conserva la forma caratteristica della A, ma con deformazione dell’immagine.
La vera novità è data dal confronto mutuale di due vocali distinte.
Fig. 7
Ritratto delle fasi della vocale U nel caso particolare di lieve chiusura delle labbra. Notare che, in questo caso, è sufficiente una dimensione di embedding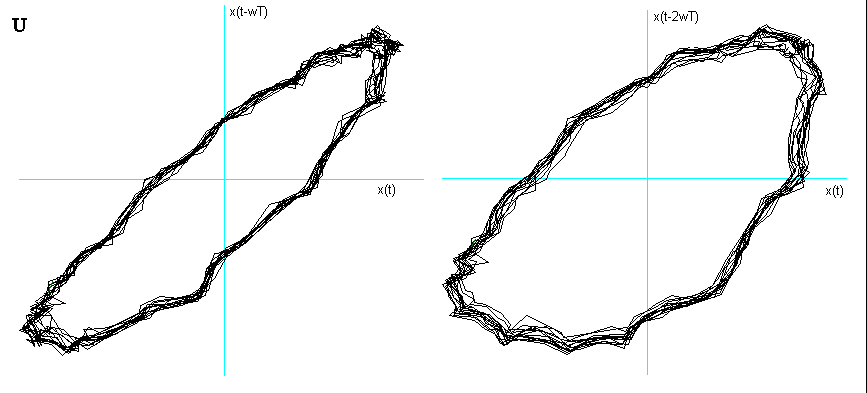
Fig. 8 Ritratto delle fasi della vocale A cantata, nella fase di quasi
stazionarietà, eseguita in due tonalità distinte (rispettivamente mib e mi).
Effettuando l’embedding con lo stesso tempo delay ![]() = 4, il suo ritratto conserva la forma caratteristica della A, ma
con deformazione dell’immagine.
= 4, il suo ritratto conserva la forma caratteristica della A, ma
con deformazione dell’immagine.

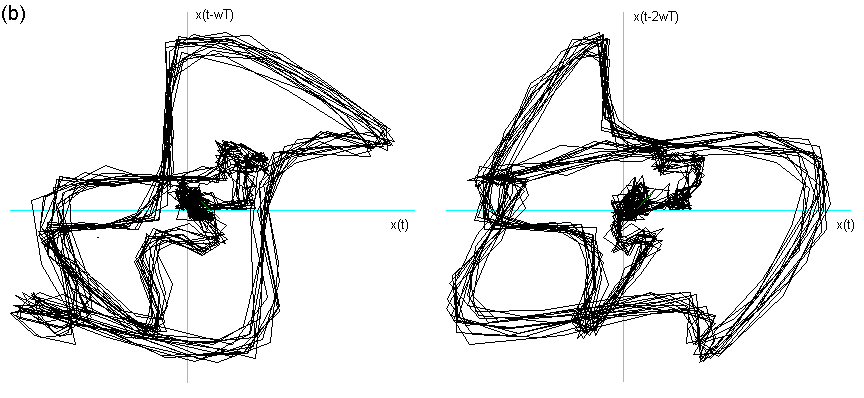
Risultati
Un primo risultato è dato, sicuramente, dalla costatazione del carattere non completamente periodico delle vocali, visibile nella fig. 7.5, rispetto all’apparente "periodicità" del segnale della fig. 7.3. Questo a riprova delle ipotesi alla base di questa ricerca.
Confrontando due vocali differenti prodotte dallo stesso apparato di fonazione e nella stessa tonalità, si osserva un fatto sorprendente: a volume maggiore del tratto vocale finale percorso dal segnale corrisponde un volume, racchiuso dalle orbite del ritratto delle fasi, maggiore. Ovvero esiste una corrispondenza tra i due volumi come negli spazi delle fasi ottenuti da equazioni differenziali invece che dal segnale.
Per esempio, nel produrre la vocale A e successivamente la E, restringiamo il tratto vocale ed abbiamo l’impressione di inserire la E "dentro" la A; questa "immagine sensoriale" diventa visibile nello spazio delle fasi.
Limitando, con la tecnica vocale, la variazione di apertura alla zona del tratto vocale comprendente la parte posteriore della lingua e il velo palatino, ed escludendo quindi movimenti mandibolari, delle labbra e di tutta la muscolatura esterna del volto, ho concentrato l’analisi ad una regione "abbastanza" limitata.
Dalla fig. 9 si vede come la vocale O è "contenuta" nella A, la E nella O, la I nella E, la U a "metà strada" tra la O e la I, che è proprio ciò che effettuiamo nel produrle. La U della fig. 8 chiede una dimensione di Embedding inferiore. Posso ipotizzare che questo sia dovuto al fatto che, nel generarla, ho "corretto" la pronuncia effettuando una chusura ulteriore, seppur minima, con i muscoli delle guance e delle labbra.
Un’altra ipotesi riguarda la possibilità di un legame tra la "rotondità" del ritratto delle due vocali A ed O e l’alzata del velo palatino, rispetto alla "spigolosità" delle altre vocali.
Fig. 9 Ritratti delle fasi delle vocali a confronto.
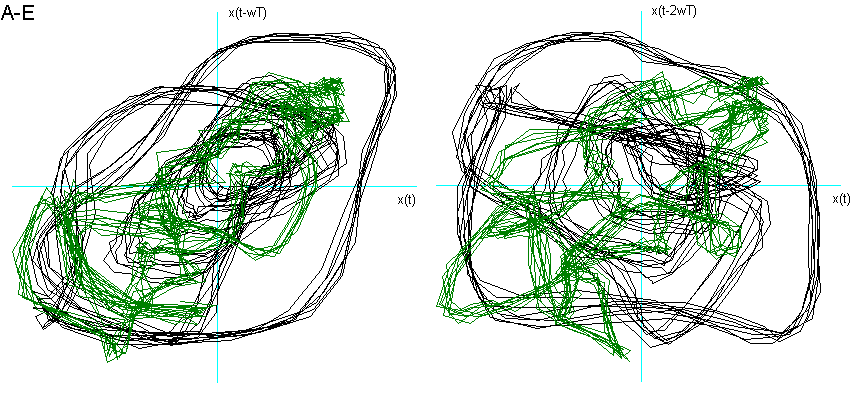
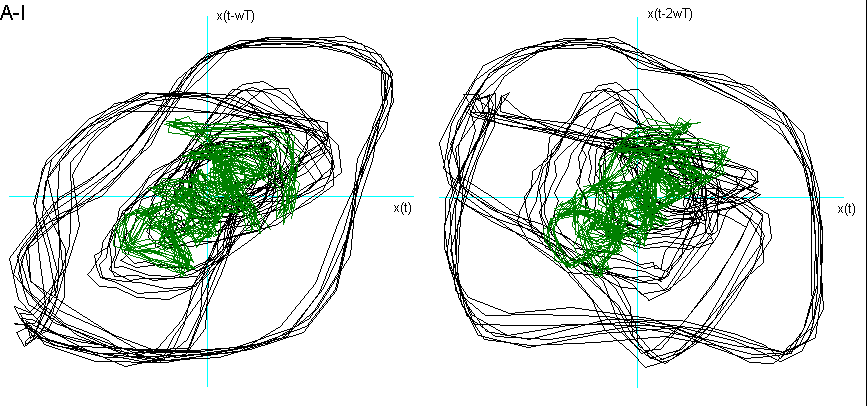
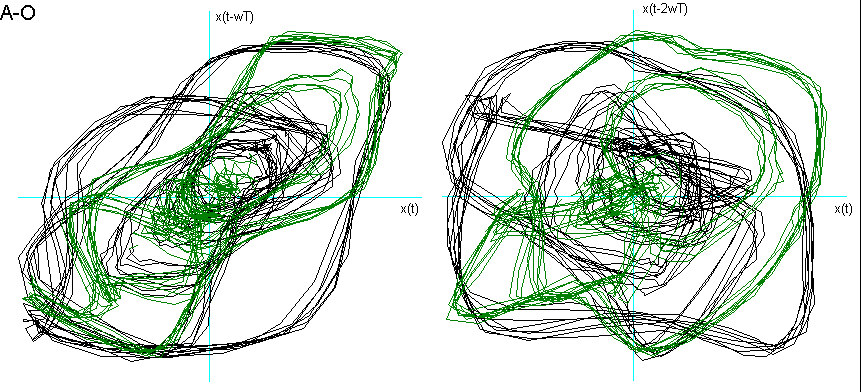
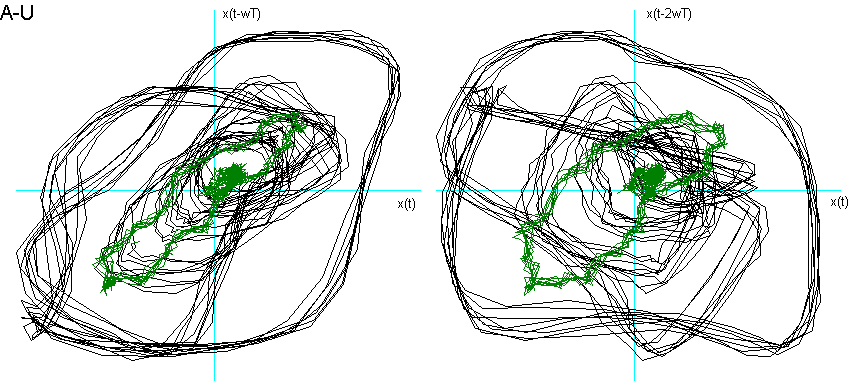
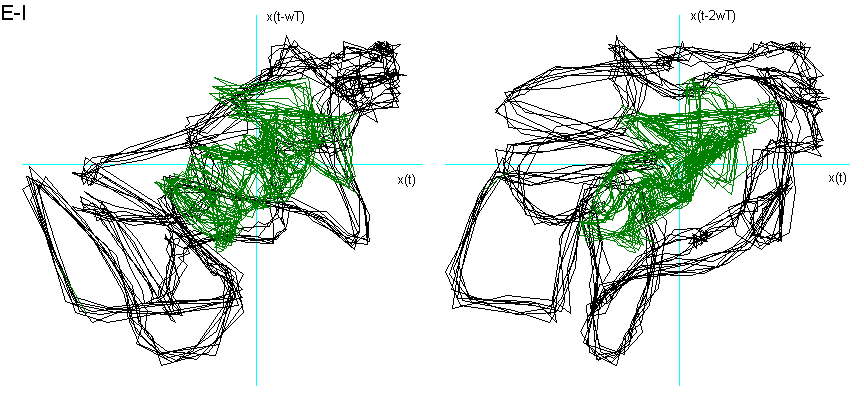
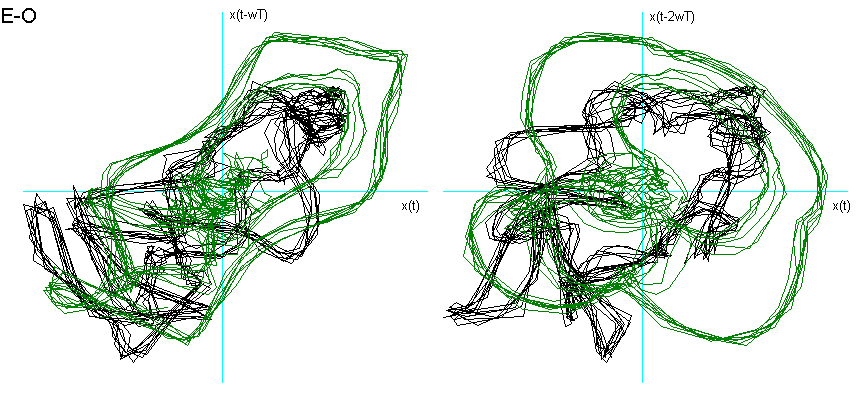
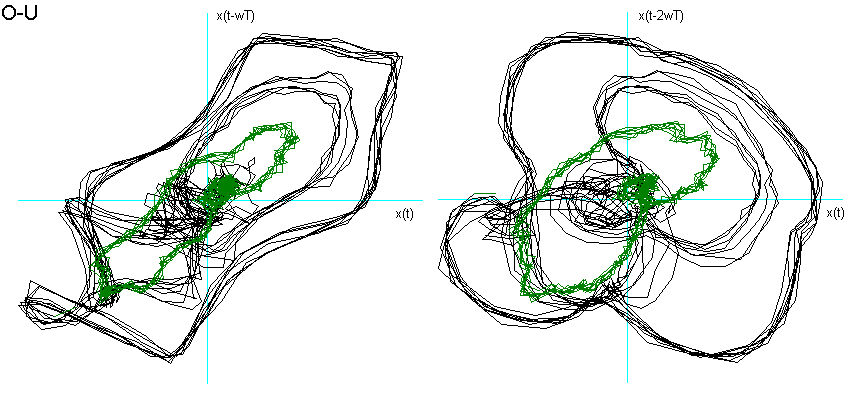
Per entrambe le ipotesi suggerirei uno studio più approfondito con verifiche ulteriori e strumentazioni più sofisticate.
Il confronto è effettuato tra i ritratti ottenuti con lo stesso
coefficiente di sfasamento. Sarebbe interessante costruire un’animazione
tridimensionale dove è possibile variare l’angolazione e il coefficiente ![]() .
.
Fig. 10 Relazione tra le aperture diverse del tratto vocale per determinare le vocali rappresentazione in "immersione" del relativo segnale ottenuto. Notare la differente posizione della lingua e, in particolare, il velo palatino alzato nelle vocali A ed O. Nell’immagine non è visibile, ma per produrre la O si forma un incavo nella parte superiore della lingua.

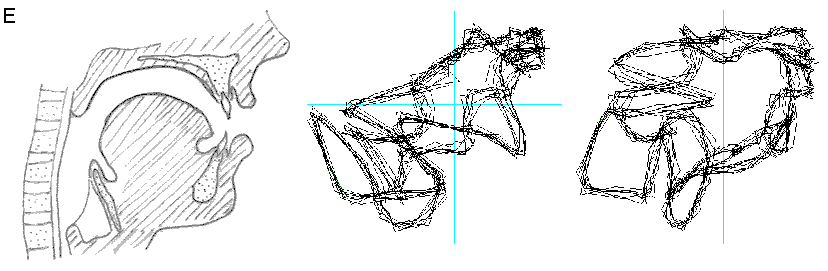
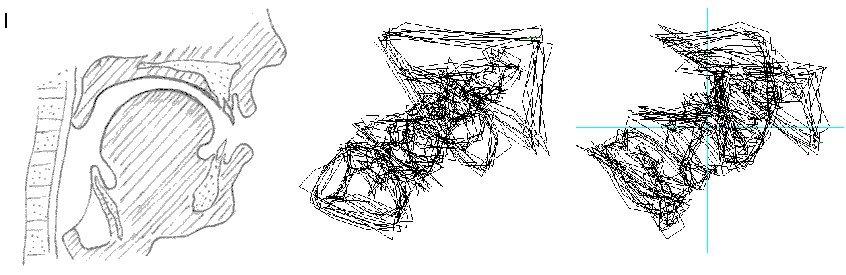
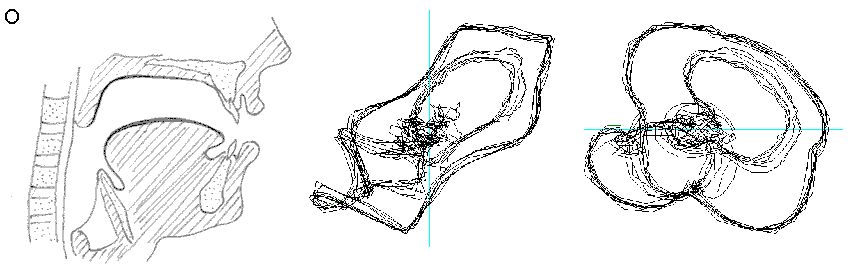

Conclusioni
L’immersione del segnale vocale in uno spazio delle fasi tridimensionale ha permesso l’individuazione della relazione tra le diverse aperture interne del tratto vocale e il volume racchiuso dalle orbite del ritratto delle fasi.
Il presente lavoro vuole essere uno spunto per ricerche successive, allargando il campo a segnali vocali prodotti da più soggetti distinti, che presentano inevitabilmente delle diversità dovute al diverso timbro vocale e gestione della voce, e a tutta la gamma delle consonanti, della pronuncia, delle innumerevoli relazioni tra vocali e consonanti, al comportamento del segnale emesso in diverse tonalità , ecc.
Auspichiamo che negli anni futuri ci saranno studi sperimentali ulteriori che svelino il funzionamento reale dell’intero apparato vocale e speriamo caldamente di aver contribuito a fare un passo avanti in tale ricerca e di aver stimolato il lettore ad approfondire l’argomento.
Allego la bibliografia completa della tesi.
Bibliografia
[Ab] Abarbanel H.D.I. (1996). Analysis of observed chaotic data. Springer.
[A.A.] Amaldi E., Amaldi G. (1972). La fisica per i licei scientifici vol.2. Zanichelli. Bologna.
[Bar] Barlow W. (1981). Il principio di Alexander. Celuc libri. (orig: 1973. The Alexander principle. The revolutionary tecnique that has helped thou sounds).
[Ben] Benettin G. et al. (1980). Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them, in "Meccanica". 15, 9.
[Bus] Busca M. (1998). Stile di gestione dell’aggressivita’ e condizione narcisistica in soggetti affetti da disfonia disfunzionale. Tesi di laurea in psicofisiologia clinica. Fac. di Psicologia. Univ. di Roma "La Sapienza".
[C.S.Y.] Casdagli M., Sauer T., Yorke J.A. (1991). Embedology. Journal of Stat. Phys.,65.
[C.F.T.V.] Celletti A., Froeschlè C., Tetko I.V., Villa A.E.P. Deterministic behaviour of short time series, preprint.
[E.R.] Eckmann J.P., Ruelle D. (1985). Ergodic theory of chaos and strange attractors. Reviews of Modern Physics, 57 : 617.
[G.K.S.] Gettys W.E., Keller F.J., Skove M.J. Fisica classica e moderna vol.1. Mc Graw Hill.
[Gua] Guardabassi G. Elementi di controllo digitale. Clup. Città’ studi. Milano. 19-33.
[G.H.] Guckenheimer J., Holmes P. (1983). Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Applied mathematical sciences 42. Springer-Verlag.
[Hec] Hecht E. Fisica 1. Zanichelli.
[ISEF] Ist. Sup. Stat. di Educaz. Fisica. (1988). La voce e il corpo. Una ricerca sui cantanti lirici. Dir. Marinotti G., a cura di Mosca L.
[Kan] Kantz H. (1994). A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett A 185. 77-87.
[LH.A.] Le Huche F., Allali A. (1993). La voce. Anatomia e fisiologia degli organi della voce e della parola. Masson. Milano.
[L.L.] Lichtenberg A.J., Lieberman M.A. (1983). Regular and chaotic dynamics. Applied mathematical sciences 38. Springer-Verlag.
[Man] Mané R., Rand D., Young L.S., editors. (1981). Dynamical systems and turbulence, Warwick,1980. Springer. Berlin.
[Mau] Maurizi M. (1998). Sindromi e malattie otorinolaringoiatriche: basi anatomofunzionali, patologiche e cliniche. 2° Ed. Piccin. Padova.
[Mull] Mullin T. The nature of chaos. Oxford science Publication.
[Mol] Molenda M. Tracking group background vocals. Keyboard. N. 11. November 1998.
[Mul] Mullin T. (1993). Disordered fluid motion in a small closed system. Phys. D 62. 192-201 North Holland.
[Nas] Nasini P. Il canto e le tecniche vocali avanzate. Seminario per "Ente Teatro Emilia Romagna". 1-5 marzo 1999. Modena.
[Nic] Nicolao U. (1999). L’emissione sonora da uno strumento musicale e la sua ripresa ravvicinata. Sound & Lite n.16, 91-92; n.17. 84-85. La fine arte della disposizione dei microfoni nella ripresa sonora. Sound & Lite n.15, 82-83.
[Nos] Noselli G. (1999). Acustica, psicoacustica, tecnologie audio e dintorni. Sound & Lite n.17. 8-10.
[Ott] Ott E. (1993). Chaos in dynamical systems. Cambridge University press.
[P.C.F.S.] Packard N.H., Crutchfield J.P., Farmer J.D., Shaw R.S. (1980). Geometry from a time series. Phys. Rev. Lett.,45.
[Ric] Ricciuti V.(1987). L’acchiappasuoni parte I. Tutto strumenti musicali, suppl. a Fare Musica n.78. Ricordi. 46-82.
[R.R.] Rodriguez R. Le consonanti nella tecnica vocale. Voci di Testa. 9 febbr.1999.
[R.C.D.] Rosenstein M.T., Collins J.J., de Luca C.J. (1993). A pratical method for calculating largest Lyapunov exponents from small data sets. Phys. D 65. 117-134.
[Shi] Shiryaev A.N. (1984). Probability. Graduate texts in mathematics 95. Springer.
[Sun] Sundberg J. (1977). The acoustics of the singing Voice. The physics of music. Scientific American. 13-14, 16-23.
[Tak] Takens F. (1981). Detecting strange attractors in turbulence. In: Dynamical systems and turbulence (ed. D.A. Rand e L.S. Young). Springer, Berlin.
[Vulp] Vulpiani A. (1994). Determinismo e caos. La Nuova Italia Scientifica. Roma.
[W.S.S.V] Wolf A., Swift J.B., Swinney H.L., Vastano J.A. (1985). Determining Lyapunov exponents from a time series. Phys. 16 D. 285-317.