|
Ultimo aggiornamento:
Gennaio 18, 2011
|
TN1 - Introduzione alla teoria dei numeri |
Docente: Marco FontanaEsercitatore: Martina Lanini Tutore: Elisa Di Gloria
|
|
Scheda del corso (dal Diploma Supplement) Congruenze e polinomi. Equazioni diofantee lineari in due (o più) indeterminate. Risoluzione di sistemi di congruenze lineari. Congruenze polinomiali. Congruenze polinomiali mod p: teorema di Lagrange. Approssimazione p-adica. Esistenza di radici primitive mod p. Indice relativamente ad una radice primitiva. Congruenze quadratiche. Residui quadratici. Simbolo di Legendre. Lemma di Gauss e Legge di Reciprocità Quadratica. Simbolo di Jacobi. Interi somma di due quadrati. Lemma di Thue. Interi rappresentabili come somma di due, tre, quattro quadrati. Funzioni moltiplicative. Le funzioni φ, σ, τ, e μ. La formula di inversione di Möbius. Studio di alcune equazioni diofantee. Il corso è rivolto gli
studenti della laurea triennale, interessati a tematiche di algebra,
teoria dei numeri e crittografia. link al portale didattico di ateneo>>
Bibliografia essenziale Ulteriori riferimenti bibliografici
|
Sommario
Vai direttamente a:
|
|
Bacheca elettronica del corso - avvisi |
![]()
![]()
![]() Verbalizzazione dell'Esame, prova scritta dell'Appello C
Verbalizzazione dell'Esame, prova scritta dell'Appello C
Lunedi' 24 Gennaio 2011, ore 11, Stanza 204
Avvisi precedenti
-
Prossimo appello d'esame: Appello C, 11 Gennaio 2011 - 10:00
Prenotazione obbligatoria sul sito di Ateneo entro il 3 Genaio 2011
(ATTENZIONE: senza prenotazione non potra' essere emesso il verbale d'esame)
- Verbalizzazione dell'Esame, prova scritta dell'Appello B
(e studenti che non hanno ancora verbalizzato il voto ottenuto con la valutazione in itinere):
Martedi' 6 Luglio 2010, ore 11, Stanza 204
- Prossimo appello d'esame: Appello X, 3 Settembre 2010 - 10:00
Prenotazione obbligatoria sul sito di Ateneo entro il 26 Agosto
(ATTENZIONE: senza prenotazione non potra' essere emesso il verbale d'esame)
-
Verbalizzazione dell'Esame, con la votazione ottenuta con le prove di esonero o con la prova scritta
dell'Appello A:
Giovedi'10 Giugno 2010, ore 11, Aula 009
-
Il secondo appello d'esame del corso, Appello B, avra' luogo l'1 Luglio ore 10.
Prenotazione obbligatoria sul sito di Ateneo (senza prenotazione non potra' essere emesso il verbale d'esame)
- Il primo appello d'esame del corso, Appello A, avra' luogo il 9 Giugno ore 10.
Prenotazione obbligatoria sul sito di Ateneo (senza prenotazione non potra' essere emesso il verbale d'esame)
- La seconda prova di valutazione in itinere del corso TN1 (II esonero) avra' luogo
Lunedi' 31 Maggio, ore 10
Prenotazione obbligatoria sul web studenti entro il 26 Maggio ore 20.
web studenti
-
Giovedi' 20 Maggio non ci sara' lezione (dalle 11 alle 13).
Venerdi' 21 maggio ci saranno due ore di esercitazione (Dr. M. Lanini) dalle 14 alle 16 in Aula B-3.
- Lunedi' 19 Aprile 2010 non si terra' il Tutorato.
- Nella settimana dal 12 al 17 Aprile e' prevista la sospensione dell'attivita' didattica
per lo svolgimento delle prove di valutazione in itinere.
- La prima prova di valutazione in itinere del corso TN1 (I esonero) avra' luogo
Lunedi' 12 Aprile, ore 10 aule G ed F
Prenotazione obbligatoria sul web studenti entro il 7 Aprile ore 20.
web studenti
- Nella settimana dal 5 al 10 Aprile, l'attivita' didattica prevista e' la seguente:
Giovedi' 8 Aprile 11-13 Lezione,
Venerdi' 9 Aprile dalle 14, prima Esercitazioni e, poi, Tutorato.
- Didattica del corso TN1 nella settimana 15-19 Marzo
LU: tutorato 16-18; MA: lez/esercitazione 14-15; GI: nessuna didattica; VE: esercitazione 14-15
|
Diario della didattica ed appunti aggiornati delle lezioni |
|
Appunti aggiornati delle lezioni |
|
Esecitazioni - Esercizi per casa |
Gli esercizi per casa vengono segnalati a lezione e sono riportati in una sezione apposita alla fine di ciascun argomento
degli appunti delle lezioni.
|
Esempio di
soluzione ... non soddisfacente |
Una ... pseudo-dimostrazione |
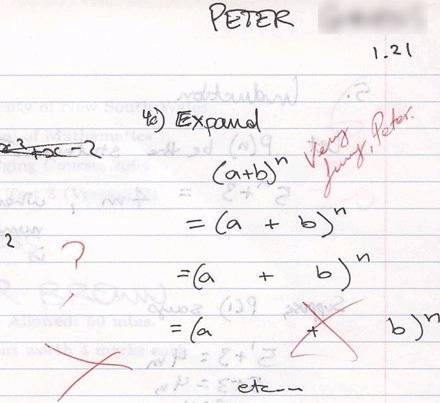 |
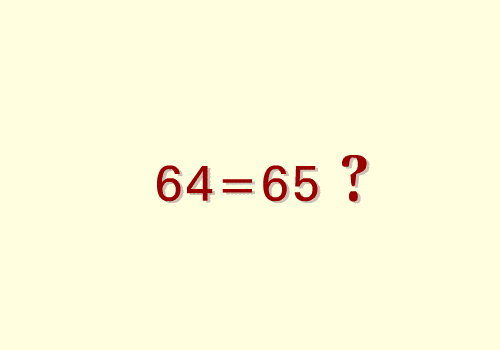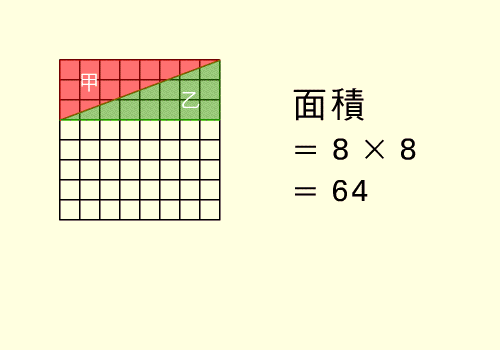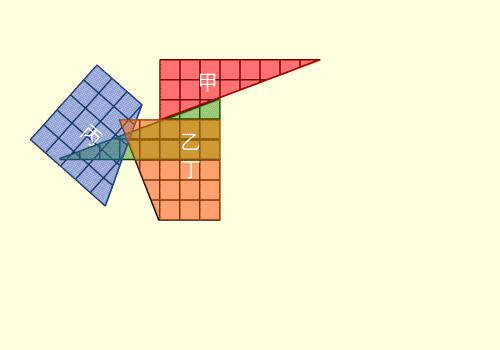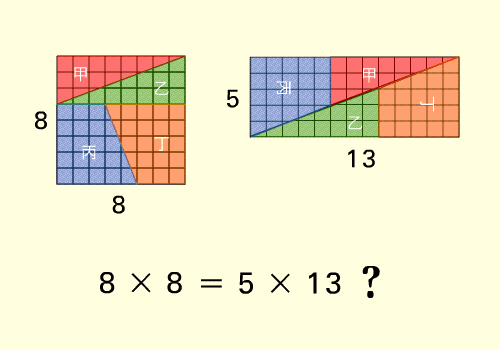 |
|
Testi degli
esercizi proposti in classe (dott.ssa
Martina Lanini) |
|
| II Settimana | |
| III Settimana | |
| V Settimana | |
| VI Settimana | |
| VII Settimana | |
| VIII Settimana | |
| IX Settimana | |
| X Settimana | |
| XI Settimana | |
|
Tutorato - Esercizi in classe |
|
Testi degli
esercizi proposti in classe (Tutore:
Elisa Di Gloria) |
|
| II Settimana | |
| III Settimana | |
| IV Settimana | |
| V Settimana | |
| VI Settimana | |
| VII Settimana | tutorato verra' recuperato in prossimita' del II esonero |
| VIII Settimana | |
| IX Settimana | |
| X Settimana | |
| XI Settimana | |
| XII Settimana | |
|
Valutazione in itinere |
|
La valutazione del profitto verrà effettuata di preferenza durante il semestre. Gli studenti frequentanti saranno invitati a svolgere periodicamente esercizi per casa (che verranno proposti durante le lezioni). Durante il tutorato verrà fornito supporto anche per la risoluzione degli esercizi per casa. Inoltre sono previste una prova scritta a metà semestre ed una prova scritta a fine semestre. Gli studenti che hanno sostenuto con esito positivo, nel corso del semestre, le prove di valutazione parziale (prove scritte) accedono direttamente al colloquio di verbalizzazione del voto proposto dal docente, da effettuarsi durante la I Sessione di esame (Appello A o B ). Per tutti gli studenti che non si avvalgono della possibilità della valutazione del profitto durante il corso, l'esame finale consiste in una prova scritta sul programma complessivo del corso.
|
|
I Prova di valutazione
(esonero) |
|
| testo e soluzioni | |
| valutazione | |
|
II Prova di valutazione
(esonero) |
|
| testo e soluzioni |
|
| |
|
|
Risorse didattiche reperibili on-line |
dal sito MIT (Massachusetts Institute of Technology)
dal sito Number Theory Web (mirror a Roma Tre)
courses in number theory: lecture notes list
in particolare, i seguenti links portano ad appunti di corsi di contenuto simile al corso TN1
- Elementary number theory (WWWL Chen, Imperial College, University of London)
- Number Theory (Pete L. Clark, University of Georgia, Athens)
- Math 780: Elementary Number Theory, Notes by Michael Filaseta, 1997, University of South Carolina
- Course Notes for elementary and algebraic number theory, local fields, Ivan Fesenko (University of Nottingham)
- Elementary Number Theory, by Peter Hackman (Linköpings Universitet)
- Lecture notes on elementary number theory (Bruce Ikenaga, Millersville University, PA)
- MP313 and MP473 number theory course notes, problems and solutions by Keith Matthews (University of Queensland)
- Maple tutorial for elementary Number Theory (Don Rideout, Newfoundland, Canada)
- Lecture notes on elementary number theory (David Santos, Community College, Philadelphia)
- Elementary Number Theory (Course notes by William Stein Harvard University)
- Introductory number theory (M. Stoll, Jacobs University)
- Notes on elementary number theory (David Wilkins, Trinity College, Dublin)
dal sito Göttingen Digitalisierung Zentrum
- Disquisitiones Arithmeticae di Carl Friedrich Gauss (l'intero volume in formato digitale)
|
The Disquisitiones Arithmeticae is a textbook of number theory written by German mathematician Carl Friedrich Gauss and first published in 1801 when Gauss was 24. In this book Gauss brings together results in number theory obtained by mathematicians such as Fermat, Euler, Lagrange and Legendre and adds important new results of his own. Scope The Disquisitiones covers both elementary number theory and parts of the area of mathematics that we now call algebraic number theory. However, Gauss did not explicitly recognise the concept of the group that is central to modern algebra, so he did not use this term. His own title for his subject is Higher Arithmetic. In his Preface to the Disquisitiones Gauss describes the scope of the book as follows: The inquiries which this volume will investigate pertain to that part of Mathematics which concerns itself with integers. Contents The book is divided into seven sections, which are: Section
I. Congruent Number in General Sections I to III are essentially a review of previous results, including Fermat's little theorem, Wilson's theorem and the existence of primitive roots. Although few of the results in these first sections are original, Gauss was the first mathematician to bring this material together and treat it in a systematic way. He was also the first mathematician to realise the importance of the property of unique factorisation (sometimes called the fundamental theorem of arithmetic), which he states and proves explicitly. From Section IV onwards, much of the work is original. Section IV itself develops a proof of quadratic reciprocity; Section V, which takes up over half of the book, is a comprehensive analysis of binary quadratic forms; and Section VI includes two different primality tests. Finally, Section VII is an analysis of cyclotomic polynomials, which concludes by giving the criteria that determine which regular polygons are constructible i.e. can be constructed with a compass and unmarked straight edge alone. Gauss started to write an eighth section on higher order congruences, but he did not complete this, and it was published separately after his death. The
Disquisitiones was one of the last mathematical works to be written in
scholarly Latin (an English translation was not published until 1965:
Carl Friedrich Gauss tr. Arthur A. Clarke: Disquisitiones Aritmeticae,
Yale University Press, 1965 ISBN 0-300-09473-6). Importance Before the Disquisitiones was published, number theory consisted of a collection of isolated theorems and conjectures. Gauss brought the work of his predecessors together with his own original work into a systematic framework, filled in gaps, corrected unsound proofs, and extended the subject in numerous ways. The logical structure of the Disquisitiones (theorem statement followed by proof, followed by corollaries) set a standard for later texts. While recognising the primary importance of logical proof, Gauss also illustrates many theorems with numerical examples. The Disquisitiones was the starting point for the work of other nineteenth century European mathematicians including Kummer, Dirichlet and Dedekind. Many of the annotations given by Gauss are in effect announcements of further research of his own, some of which remained unpublished. They must have appeared particularly cryptic to his contemporaries; we can now read them as containing the germs of the theories of L-functions and complex multiplication, in particular.
|
Programma finale del corso,
A.A. 2009/2010 ![]()
Appello A: 9 Giugno 2010 - 10:00
Appello B: 1 Luglio 2010 - 10:00
Appello X: 3 Settembre 2010 - 10:00
Appello C: 11 Gennaio 2011 - 10:00
| testo e soluzioni | |
| valutazione | |
|
|
